在工程设计和分析的现代实践中，有限元分析（fea）已经成为一种常用的工具，能够模拟和预测在不同条件下的材料和结构的性能。然而，对于许多工程师来说，高数是他们学术生涯中最令人畏惧的一部分。那么，学习有限元分析需要深厚的数学基础吗？让我们听听仿真工程师是怎么说的。
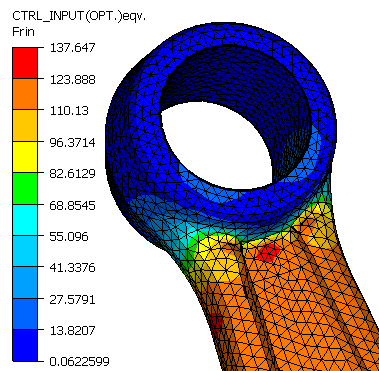
首先，理解有限元分析的基本原理，需要一定的数学基础。然而，这并不意味着需要彻底掌握高数。高数知识在有限元分析中的应用主要涉及微积分、线性代数和微分方程等部分。这些数学知识是构建和理解有限元分析模型的基础。
仿真工程师表示，如果你对这些数学概念有基本的理解，并能将其应用到实际问题中，你仍然可以在有限元分析领域取得成功。深入的数学掌握可以在解决更复杂的有限元问题时提供更大的帮助，但对于一些基本的分析任务，你仍然可以依靠软件工具进行操作。
然而，对于想要成为高级仿真工程师的人来说，深入理解高数知识是必不可少的。这是因为高级的有限元分析需要更复杂的数学模型和更深入的理论理解。对于这些复杂问题，只有深入理解相关的数学知识，才能准确地构建模型，并解读和分析结果。
此外，高数知识也有助于理解如何优化有限元分析过程。比如，了解微积分的知识可以帮助你调整模型参数以改善结果的精度；理解线性代数可以让你更好地理解和使用矩阵运算来简化计算过程。
总的来说，学习高数对于有限元分析的学习和实践并不是必须的，但对于想要成为高级仿真工程师的人来说，掌握高数无疑是有帮助的。仿真工程师建议，如果你的工作涉及到高级的有限元分析，或者你希望在这个领域有更深入的研究和发展，那么你应该投入时间和精力去学习和深入理解高数。
此外，高数的掌握不仅能帮助你更好地理解和应用有限元分析，还能提升你的职业发展潜力。许多工程和科研职位都需要对高数有深入的理解，因为它是一切科学和工程实践的基础。
然而，如果你只是在有限元分析的入门阶段，或者你的工作只需要处理基本的分析任务，那么你并不需要具备深厚的高数知识。你仍然可以通过学习和实践来提升你的有限元分析技能，并依靠软件工具来完成大部分的工作。
总的来说，学习高数对于有限元分析的学习和实践确实有帮助，但这并不是不可逾越的障碍。只要你有决心和毅力，你一定可以在这个领域取得成功。所以，不要被高数吓倒，勇敢地迎接挑战，让我们一起在有限元分析的道路上不断前进！
