abaqus软件分析指南285：允许abaqus/cae选择错误目标-凯发网站

允许abaqus/cae选择错误目标

如果您指定了最小/最大错误控制方法而没有设置错误目标，abaqus/cae会自动选择错误目标nmax和nmin·在先前的remesh迭代分析中，这两个目标都被计算为误差指示器结果的一小部分。自自动误差目标缩减对于网格细化研究是一个很好的选择，在这种研究中，您没有特定的误差目标，但希望查看网格细化对结果的影响。

 

abaqus/cae用法：网格模块：创建重新网格化规则：调整大小方法：错误目标;选择自动减少错误目标

 

指定错误目标

作为自动减少错误目标的替代方法，您可以指定两个错误目标，7max和7min。图2说明了这两个位置。7max应用于元素i,7min应用于元素j。使用两个误差目标的值，abaqus/cae应用一种尺寸确定方法，试图在它们各自的位置同时满足7min和7/max.

abaqus/cae用法：网格模块：创建重新网格化规则：调整大小方法：错误目标;选择“固定错误目标”;输入最大基本凯发网站的解决方案错误指示器目标7max和最小基本凯发网站的解决方案错误标识器目标nmin

 

偏倚因素

您可以使用重新网格化规则中的偏置因子定义来进一步调整大小在最大和最小基本凯发网站的解决方案位置之间的分布。偏倚因子定义remesh区域中这两个极端值之间的粒度分布梯度，如图3所示。

 

 

图3：偏置因子对元素尺寸分布的影响。

 

您可以将此因子设置在两个定性极端之间，即“弱”和“强”。在较弱的极端情况下，在远离最大基本解的位置，单元尺寸将增加得最快。在最强的极端，元素的大小将增加得最慢。默认设置是偏向于强烈的极端。

 

abaqus/cae用法：网格模块：创建重新网格化规则：调整大小方法：网格偏置;将滑块拖到“弱”和“强”之间的设置

 

均匀误差分布

均匀误差分布方法提供了一个单一的误差指标目标，n，用于控制大小。abaqus/cae应用的尺寸方法，使得在重新网格化规则区域的总误差均匀分布在所有的元素，并满足给定的误差指标的目标。该方法试图满足误差指标的目标，共同为整个重新网格化规则区域，而不是在每个元素。因此，奇异点的存在不会妨碍自适应过程实现误差目标。

 

abaqus/cae用法：网格模块：创建重新网格划分规则：调整大小方法：方法：选择均匀误差分布

允许abaqus/cae选择错误目标如果您指定了统一的错误分布方法而没有设置错误目标，那么abaqus/cae会自动选择错误目标r。在先前的remesh迭代分析中，目标被计算为误差指标结果的一小部分。自动误差目标缩减对于网格细化研究是一个很好的选择，在这种研究中，您没有特定的误差目标，但希望查看网格细化对结果的影响。

 

abaqus/cae用法：网格模块：创建重新网格化规则：调整大小方法：错误目标;选择自动减少错误目标

 

默认大小调整方法和参数

该方法的结果是应用最小/最大值控制或均匀误差分布方法的自动误差目标缩减形式，根据表1中的误差指示变量应用该方法。

 

 

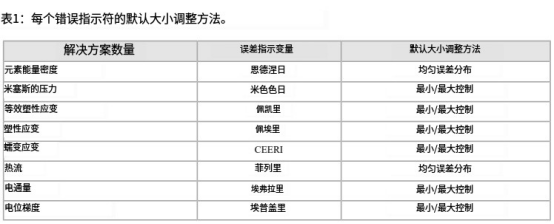
重新网格化规则引用多个错误指示器时，大小调整方法将独立应用于每个错误指示器变量，生成的局部大小基于从每个大小调整方法计算出的最小大小。

 

abaqus/cae用法：网格模块：创建重新网格划分规则：调整大小方法：方法：选择默认方法和参数

 

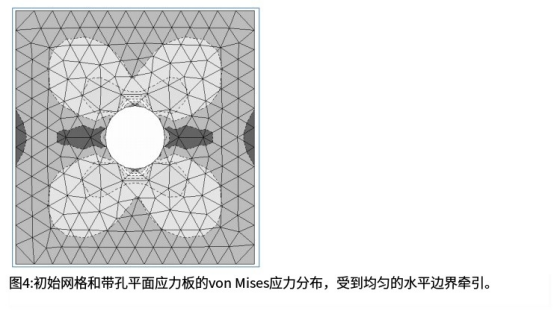
示例：带有圆形应力立管的板

通过一个简单的例子说明了最小值/最大值控制和均匀误差分布方法的基本行为之间的区别。图4显示了带有孔的板的简单载荷的应力结果。

 

 

 

最小/最大控制

图5说明了当用户选择最小/最大控制方法并指定两个误差目标(7min和7max)时，abaquscae生成的自适应网格。在本例中1min=5%和7max=1%，并且网格偏移设置为默认设置。这些设置导致网格紧紧围绕孔(应力梯度)，同时平滑地过渡到远离孔的相对粗糙的网格。

 

 

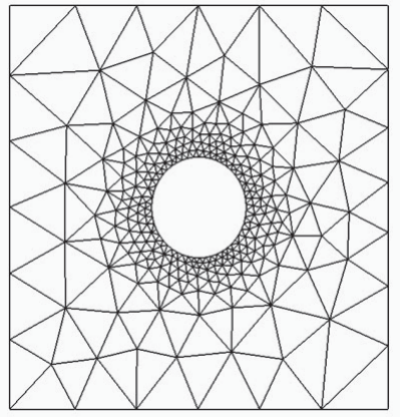
图5：最小/最大控制尺寸方法产生的自适应重新网格。

 

均匀误差分布

图6说明了当用户选择均匀误差分布方法并指定单一均匀误差指示器目标(7)时，abaqus/cae生成的自适应网格。在本例中n=1%。此设置的结果是网格集中在孔(应力梯度)周围，同时也细化了应力较小区域的网格。

 

 

 

其他重新网格化规则设置的影响

在创建重新网格化规则时指定大小调整方法，大小调整方法在自适应重新网格化过程中计算新的元素大小。但是，重新网格化规则中的以下其他设置可能会影响abaqus/cae生成的网格，而与您选择的大小调整方法无关：

l区域选择，

l步和帧的选择，

l尺寸的限制，

l近似最大元素数，以及

l细化和粗化速率因素。

 

区域选择

大小调整方法是跨元素集定义的，对应于在abaqus/cae中应用网格重划规则的区域。在每一组元素中，abaqus/cae将调整大小操作应用到重新网格化规则中指定的错误指示器变量。大小调整操作的结果基于整个单元计算到最近节点的外推，并且结果是基于节点的。

abaqus/cae用法：网格模块：创建重网格规则：编辑区域

 

步长和帧选择

abaqus仅从指定步骤中的最后一个可用帧对错误指示符变量应用大小调整操作。有关步长、帧和误差指示器的选择如何影响您在瞬态分析中捕捉响应的能力的讨论，请参见误差指示器特征。

 

abaqus/cae用法：网格模块：创建重新网格化规则：步骤和指示器：步骤;选择要应用规则的步骤

 

袋

网格模块：创建重新网格化规则：步长和指示器：输出频率;选择步长的最后增量或步长的所有增量

 

大小限制

创建重新网格化规则时，可以通过指定大于或小于为重新网格规则区域定义的大小约束的元素来约束调整大小操作。abaqus/cae为这些约束提供默认设置。

 

·默认最小元素大小约束为应用重新网格化规则的零件实例的默认边界种子大小的1%。

默认的最大元素大小约束是应用重新网格化规则的零件实例的默认边界种子大小的10倍。

abaqus/cae用法：网格模块：创建重新网格化规则：约束：元素大小

 

近似最大元素数

对于重新网格化规则，您可以指定最大元素数的近似限制。借由使用此限制，您可以控制分析的成本，并确保不会建立过大的网格。如果在定义此约束时，目标错误需要的元素超过指定的限制，则abaous/cae将在内部减少目标错误，以便生成的元素大致满足指定的元素计数。使用此约束可能会阻止自适应过程实现错误目标。默认情况下，此约束不处于活动状态。

 

abaqus/cae用法：网格模块：创建重新网格化规则：约束：近似最大元素数

 

细化和粗化速率因子

您指定的细化和粗化因子根据网格的选代更改定义了对网格大小的约束。这些因素调节施胶方法的侵略性。细化因子控制网格的细化或引入更小的元素。粗化因子控制网格的粗化或引入更大的元素。abaqus/cae为这些速率因子提供了默认设置，这些设置旨在防止在单个重新网格迭代中过度粗化或过于昂贵的细化。

 

细化因子对自适应网格划分过程的收敛性有显著的影响。一旦您确定了适合您的应用程序的尺寸方法参数，您就可以通过增加细化因子来实现更快和更有效的网格收敛。但是，在您的自适应过程没有很好地收敛的情况下，增加的细化因子可能会导致重新网格迭代中元素的过度增加

 

abaqus/cae用法：网格模块：创建重新网格化规则：约束：速率限制

 

协调重叠网格重划规则

abaqus/cae对与您的重新网格化规则相关联的区域或步骤没有任何限制。您可以应用多个重新网格化规则，因此，大小函数在同一时间到相同的区域。类似地，您可以指定彼此重叠的重新网格化规则。当abaqus/cae生成新的网格时，它会考虑所有位置的所有网格重划规则，并使用最小的计算单元尺寸来驱动网格生成算法。

 

温馨提示：

此文档为达索官方英文文档翻译，尽管我们已经尽力确保准确性，但在翻译过程中可能会有一些错误或细微差别。如果想要了解官方原版，可联系客服进行索取。